Revision Notes of Chemical Reaction and Equations? (more…)
Month: December 2020
CBSE Notes Class-10 Science? CBSE Notes for Class 10 Science – Chapter wise Revision Notes Class 10th is a crucial...
NCERT Solutions For Class 10th SCIENTIFIC KNOWLEDGE / NCERT Solutions / NCERT Solutions for Class 10 NCERT Solutions for class...
NCERT Solutions for Class 10 Science National Council of Educational Research and Training (NCERT) is a self-governing organization of the...
CBSE Class 9 Science Practicals/Lab Manual To establish the relation between the loss in weight of a solid when fully...
To trace the path of a ray of light passing through a rectangular glass slab? Experiment – 9 Aim To...
To identify Parenchyma and Sclerenchyma tissues in plants from prepared slides? To identify Parenchyma and Sclerenchyma tissues in plants from...
To trace the path of the rays of light through a glass prism? Experiment – 8 Aim To trace the...
CBSE Class 10 Science Practicals/Lab manuals CBSE Class 10 Practicals play an important role in developing students knowledge. All the...
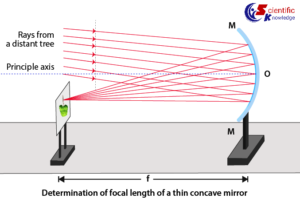
Experiment : 07 Aim To determine the focal length of: Concave mirror and Convex lens by obtaining the image of...